スポンサーリンク
ちーがくん
はかせ！地学の固体地球の単元で「偏平率」という言葉が出てきたのですが、いまいちよく分からなくて…
これってどういう意味の言葉なのか教えてください！
これってどういう意味の言葉なのか教えてください！
はかせ
いきなり偏平率と言われても、いまいちイメージが付きづらい言葉じゃな。
よし、今回は偏平率について解説するぞ！
よし、今回は偏平率について解説するぞ！
高校での地学基礎・地学の重要キーワードである「偏平率」
重要キーワードであるものの、いまいちイメージしづらくてよく分かっていない…という人も多いのではないでしょうか？
本記事を読めば、そんな分かりづらい偏平率を図解で理解できます。
今回は偏平率について、モルモットたちと一緒に学んでいきましょう！
スポンサーリンク
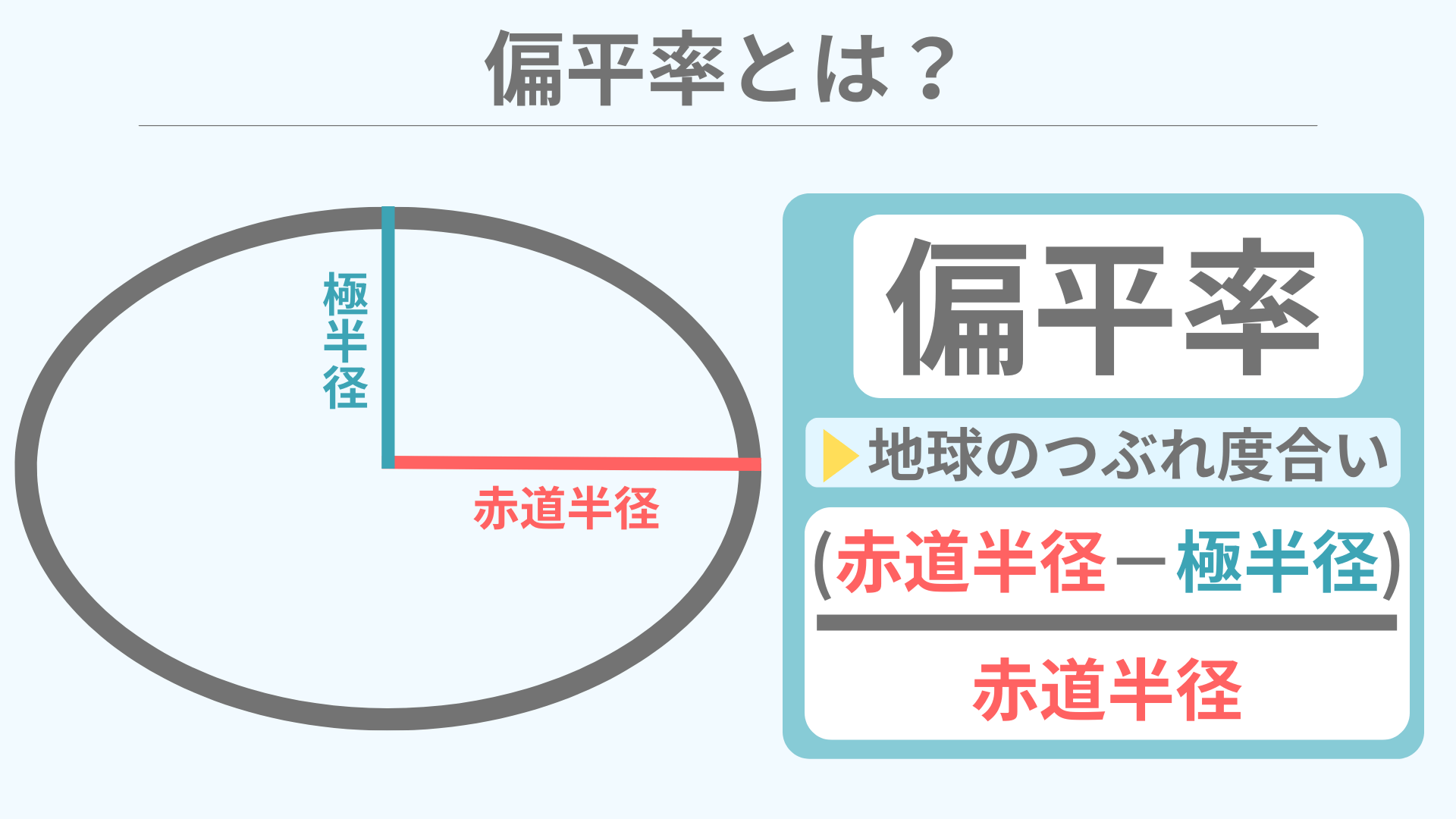
偏平率とは？
はかせ
偏平率とは一言で言うと「地球のつぶれ度合い」のことなんじゃ！
はかせ
そうなんじゃ。それが具体的にどのくらい潰れているのか？というのを表したのがこの「偏平率」なんじゃ！
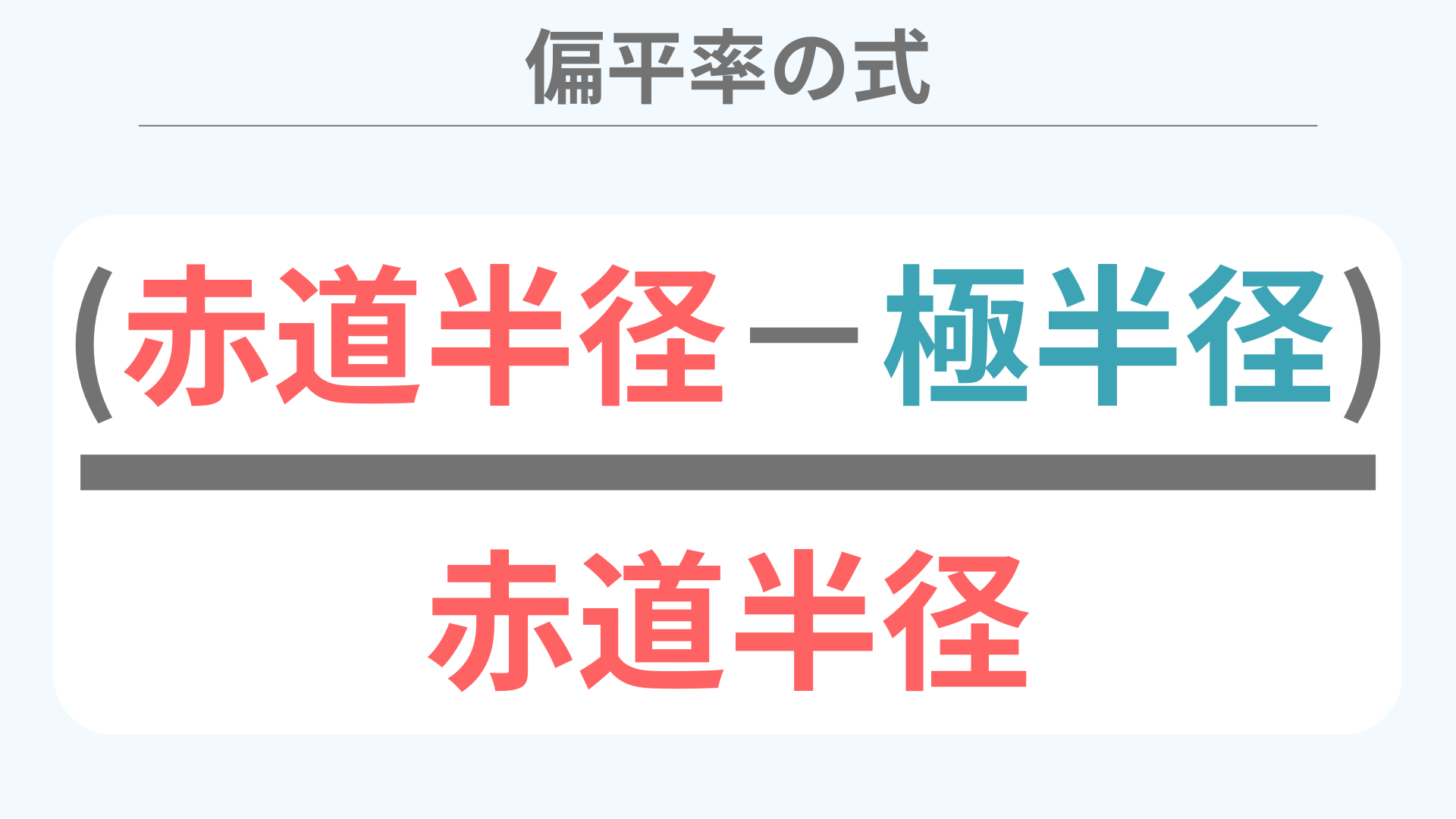
偏平率の式
ちーがくん
式では、赤道半径の長さから極半径の長さを引いて、それを赤道半径でさらに割っていますね。
これの意味がいまいち分からなくて…
これの意味がいまいち分からなくて…
はかせ
そうじゃな、確かに何を意味しているか理解しづらい式じゃ。しかしこの式の意味を理解せずにただ丸暗記しようとすると、混乱する原因になる。
このように納得できない式が出てきた場合には、極端なケースで考えてみるんじゃ！
このように納得できない式が出てきた場合には、極端なケースで考えてみるんじゃ！
ちーがくん
極端なケース？
偏平率は0に近いほど完全な球体に近い！
はかせ
例えば今回の場合では、極端なケースとして地球が完全な球体であると仮定して考えてみよう。
はかせ
地球が完全な球体である場合、赤道半径と極半径の長さが等しくなるな。
ちーがくん
あっ！そうなると(赤道半径-極半径)の部分が0になって、偏平率は0になりますね！
はかせ
そうなんじゃ。このことから、地球が完全な球体である場合には偏平率は0になるといえる。
言い換えると偏平率が0に近ければ近いほど、完全な球体に近くなるということじゃ！
言い換えると偏平率が0に近ければ近いほど、完全な球体に近くなるということじゃ！
ちーがくん
分子である(赤道半径-極半径)の部分が0に近いほど完全な球体に近くて、この部分が大きくなるほど完全な球体から遠ざかっていくイメージですね！なるほど！
実際の地球の偏平率を計算すると？
ちーがくん
こうなると気になるが「実際の地球の偏平率はどのくらいか」っていうことですよね。
実際の地球はどのくらいの偏平率で、どのくらいつぶれているといえるのでしょうか…？
実際の地球はどのくらいの偏平率で、どのくらいつぶれているといえるのでしょうか…？
はかせ
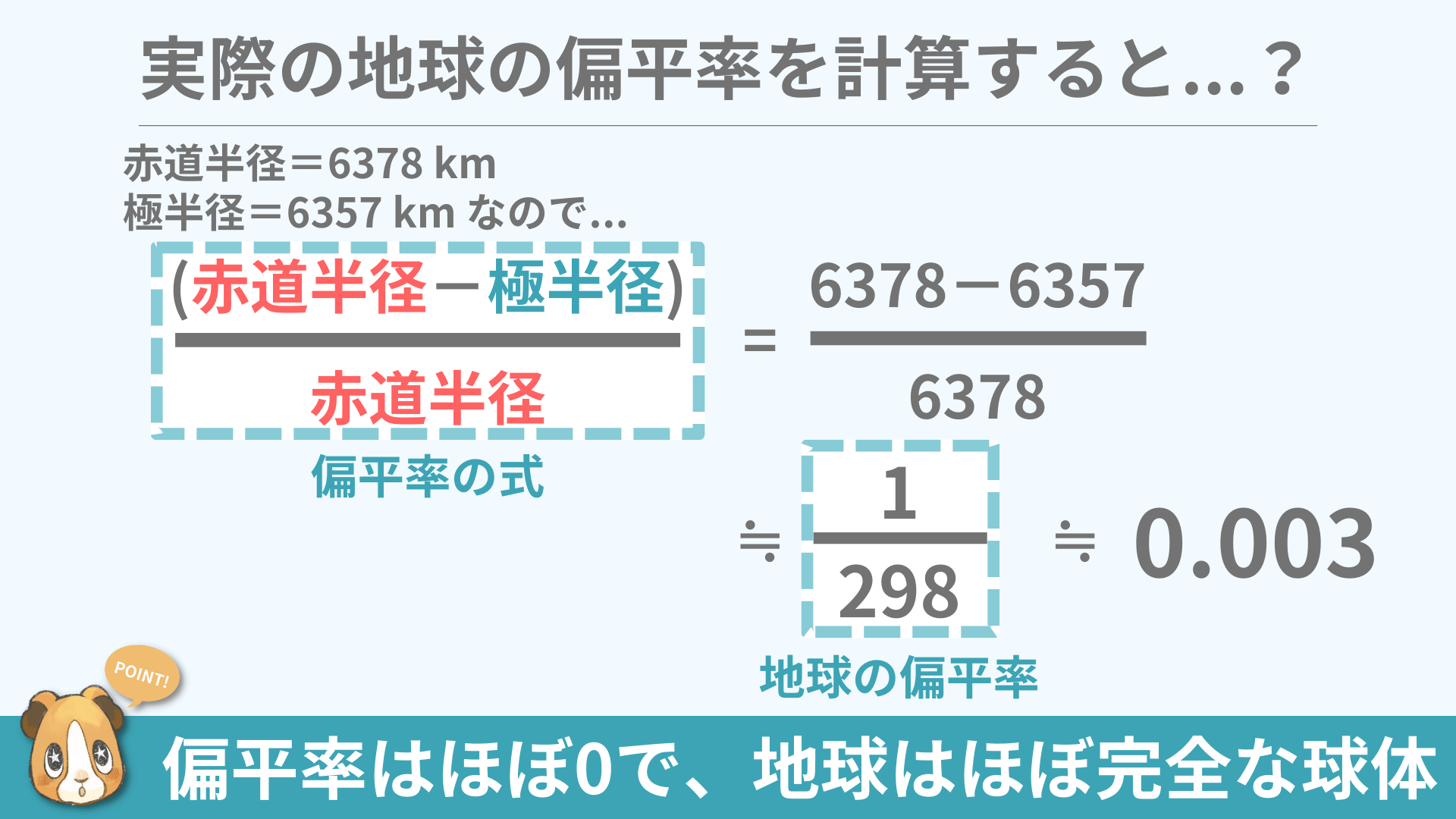
では実際に計算してみよう！
赤道半径が6378km、極半径が6357kmであるので、この数値を使って偏平率の式に当てはめて、地球の偏平率を計算してみよう。
赤道半径が6378km、極半径が6357kmであるので、この数値を使って偏平率の式に当てはめて、地球の偏平率を計算してみよう。
ちーがくん
およそ0.003!?
もうほぼ0じゃないですか！
もうほぼ0じゃないですか！
はかせ
そうじゃな。ほぼ0で、地球はほぼ完全な球体であると言ってよいじゃろう。
まとめ
はかせ
今回は、地球のつぶれ度合いを表す偏平率について解説したぞ。
定義や式を丸暗記すると混乱してしまうところじゃが、慣れればそれほど難しくないということが分かってもらえたのではないかと思うぞ。
定義や式を丸暗記すると混乱してしまうところじゃが、慣れればそれほど難しくないということが分かってもらえたのではないかと思うぞ。
ちーがくん
初めは式の意味が分からず諦めかけましたが、地球が完全な球体である場合を仮定して考えることで理解できました！しっかり復習したいと思います。
はかせ！今日はありがとうございました！
はかせ！今日はありがとうございました！
最後までお読みいただき、ありがとうございました！
スポンサーリンク
